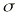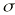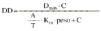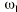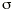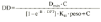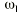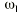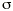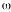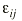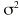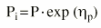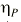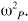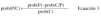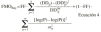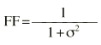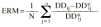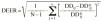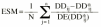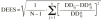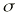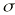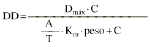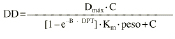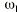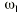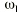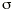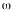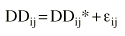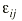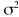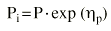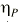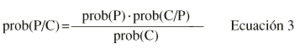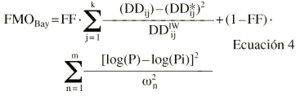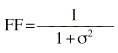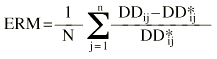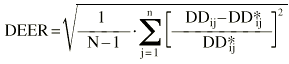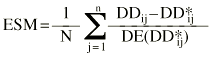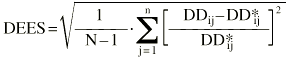ORIGINALES
ESTIMACIÓN BAYESIANA DE PARAMETROS FARMACOCINÉTICOS DE CICLOSPORINA EN PACIENTES CON TRASPLANTE RENAL
Porta Oltra, B., Especialista en Farmacia Hospitalaria;Pérez-Ruixo, J. J.,Especialista en Farmacia Hospitalaria;Galloso Rodríguez, M. A.,Especialista en Farmacia Hospitalaria;Casabó Alós, V. G.,
Doctor en Farmacia, Profesor Titular del Departamento de Farmacia y Tecnología Farmacéutica;
Jiménez Torres, N. V.,Doctor en Farmacia. Catedrático del Departamento de Farmacia y Tecnología Farmacéutica. Jefe de Servicio.
Servicio de Farmacia. Hospital Universitario Dr. Peset. Departamento de Farmacia
y Tecnología Farmacéutica. Universidad de Valencia.
Correspondencia: B. Porta Oltra. Servicio de Farmacia. Universidad Dr. Peset. Avda. Gaspar Aguilar, 90. 46017 Valencia.
Fecha de recepción: 19-5-99
Palabras clave:
Estimación bayesiana. Farmacocinética poblacional. Ciclosporina. Trasplante renal.
Resumen:
El objetivo del presente trabajo es describir un modelo farmacocinético poblacional y evaluar su capacidad predictiva, mediante un algoritmo bayesiano, en la monitorización de ciclosporina (CsA) en pacientes con trasplante renal.
La población de estudio está constituida por 33 pacientes receptores de un injerto renal. Los pacientes se asignaron a dos grupos: el grupo A, formado por 20 pacientes, se utilizó para el desarrollo del modelo farmacocinético; el grupo B, formado por 13 pacientes, se utilizó para evaluar la capacidad predictiva del modelo farmacocinético mediante la metodología bayesiana. En ambos grupos el protocolo de inmunosupresión que recibieron los pacientes incluyó la administración de CsA en triple terapia asociada a micofenolato de mofetilo (2 g/día) y prednisona (0,5-1 mg/ kg/día). La dosis de CsA se individualizó de forma progresiva en base al resultado de la concentración sanguínea valle y al ámbito terapéutico predefinido. La determinación de los niveles de CsA se realizó en sangre completa mediante un ensayo de inmunofluorescencia polarizada específico para CsA y sus metabolitos.
Para cuantificar la relación entre la dosis diaria administrada y la concentración sanguínea de CsA se compararon dos modelos estructurales basados en la ecuación de Michaelis-Menten. El modelo 1 es el modelo desarrollado por Grevel et al, donde la Km se incrementa de forma lineal a medida que transcurre el tiempo postrasplante hasta alcanzar un valor constante, y el modelo 2 se caracteriza por considerar una función creciente no lineal para describir el cambio de Km con respecto al tiempo postrasplante. En el grupo de pacientes de la población B se realizaron las predicciones de dosis diarias de CsA a través de la estimación de parámetros farmacocinéticos individuales, mediante la metodología bayesiana, utilizando como información a priori la proporcionada por el modelo 2. La exactitud y la precisión en la estimación de la dosis diaria a administrar se evaluó mediante la teoría de errores de predicción de Sheiner y Beal.
El modelo 2 describe significativamente mejor que el modelo 1 la relación entre la dosis diaria administrada y la concentración de CsA. Además, la estimación bayesiana de parámetros farmacocinéticos individuales muestra una excelente exactitud tanto de la predicción a priori como de la predicción a posteriori, ya que el error relativo medio no es significativamente distinto de 0. Además, la desviación estándar del error relativo medio de las predicciones realizadas a posteriori es significativamente menor que la alcanzada a priori. Ahora bien, el error estándar de la predicción a posteriori de la dosis diaria a administrar es excesivo para garantizar una buena precisión de la estimación.
BAYESIAN ESTIMATION OF PHARMACOKINETIC PARAMETERS OF CYCLOSPORINE IN PATIENTS WITH KIDNEY TRANSPLANTATION
Key words:
Bayesian estimate. Population pharmacokinetics. Cyclosporine. Kidney transplantation.
Summary:
A population pharmacokinetics model is described and its predictive capacity for monitoring cyclosporine (CsA) in patients with kidney implants was evaluated using a bayesian algorithm.
The study population had 33 patients who had undergone kidney transplantation. Patients were assigned to two groups: group A, 20 patients, was used to develop the pharmacokinetic model; group B, 13 patients, was used to evaluate the predictive capacity of the pharmacokinetic model using the bayesian method. In both groups, the immunosuppressant protocol that the patients received included CsA associated with mycophenolate mofetil (2 g/day) and prednisone (0.5-1 mg/kg/day). The CsA dose was individualized progressively based on trough blood concentration and the predefined therapeutic range. CsA levels were determined in whole blood by specific polarized immunofluorescence assay for CsA and metabolites.
To quantify the relation between the daily dose administered and CsA blood concentration, two structural models were compared using the Michaelis-Menten equation. Model 1 was the model developed by Grevel and colleagues, in which Km increased linearly with post-transplantation time until reaching a constant value. Model 2 used an incrasing non-linear function to describe the change in Km with respect to post-transplantation time. In the group of patients in group B, daily CsA doses were predicted by estimating individual pharmacokinetic parameters, using the bayesian method, using a priori information provided by model 2. The accuracy and precision of estimates of the daily dose were evaluated with Sheiner and Beal''s prediction error theory.
Model 2 described the relation between the daily dose and CsA concentration significantly better than model 1. The Bayesian estimate of individual pharmacokinetic parameters was accurate for prediction a priori and a posteriori, the mean relative error not differing significantly from 0. The standar deviation of the mean relative error of predictions a posteriori was significantly better than for predictions a priori. However, the standar error of the prediction a posteriori of the daily dose was too high to ensure the precision of the estimate.
INTRODUCCIÓN
El tratamiento con ciclosporina (CsA0 en pacientes con trasplante renal se caracteriza por la alta variabilidad, tanto a nivel interindividual como intraindividual, encontrada en los procesos cinéticos y dinámicos (1). Esta situación es particularmente evidente en las primeras semanas postrasplante tras la administración oral de CsA (2).
La relación establecida entre la concentración en sangre de CsA y su efecto terapéutico ha exigido la incorporación de la determinación de CsA en sangre total como un proceso más de la monitorización en el paciente trasplantado. Así, se ha demostrado la utilidad de la individualización posológica al prevenir el rechazo del órgano trasplantado, minimizar la toxicidad inherente al fármaco y/o evaluar la etiología de la disfunción del trasplante. A su vez esta práctica permite asegurar el cumplimiento del paciente y controlar diversos factores que alteran el perfil cinético del fármaco, como pueden ser las interacciones farmacológicas (3, 4).
De las técnicas propuestas de individualización posológica de CsA, la aproximación más robusta es la basada en el área bajo la curva (AUC) (5). Ahora bien, el número de muestras de sangre necesario para llevar a cabo esta estrategia dificulta su aplicación en la práctica clínica diaria a pesar de la incorporación de los modelos de estimación del AUC a partir de un número reducido de muestras (6-9). Una alternativa, a la individualización posológica basada en el AUC, es la estimación de los parámetros farmacocinéticos individuales de CsA a partir de la concentración valle de CsA mediante la utilización de la metodología bayesiana (10). Esta técnica ha demostrado su utilidad en la monitorización de aminoglucósidos, digoxina, vancomicina, teofilina, entre otros fármacos (11); sin embargo, su aplicación a la monitorización de CsA no ha alcanzado su pleno rendimiento debido a la elevada variabilidad inter e intraindividual en el comportamiento farmacocinético de CsA, fundamentalmente tras la administración de la formulación tradicional (Sandimmun®) por vía oral (12). Actualmente, la nueva presentación oral de CsA, formada por una microemulsión lipídica (Sandimmum Neoral®) presenta una menor variabilidad inter e intraindividual que la forma tradicional y ocasiona una aceptable relación lineal entre dosis administradas y el AUC (13, 14).
La aplicación de la metología bayesiana, con garantía de éxito, requiere necesariamente la correcta caracterización del comportamiento farmacocinético de CsA en una población representativa de pacientes (15). Para caracterizar el comportamiento farmacocinético poblacional de CsA es necesario cuantificar la tendencia central y la variabilidad inter e intraindividual de los parámetros farmacocinéticos, así como establecer la influencia de factores diagnósticos, demográficos y clínicos (covariables) sobre dichos parámetros (15, 16).
El objetivo del presente trabajo es describir un modelo farmacocinético poblacional y evaluar su capacidad predictiva, mediante un algoritmo bayesiano, en la monitorización de pacientes con trasplante renal.
MÉTODO
Pacientes y tratamiento inmunosupresor
La población de estudio está constituida por 33 pacientes receptores de un injerto renal. Los pacientes se asignaron a dos grupos: el grupo A, formado por 20 pacientes, se utilizó para el desarrollo del modelo farmacocinético; el grupo B, formado por 13 pacientes, se utilizó para evaluar la capacidad predictiva del modelo farmacocinético mediante la metodología bayesiana. Las características más relevantes de los pacientes de ambos grupos se muestran en la tabla 1.
| Tabla 1. Características de los pacientes del estudio | |||
| Población A (n = 20) | Población B (n - 30) | p | |
| Sexo (V/M) | 11/9 | 8/5 | -- |
| Edad (años) | 47,3 (12,8) | 47,3 (12,3) | n.s. |
| Peso (kg) | 66,4 (13,9) | 68,0 (15,6) | n.s. |
| Creatinina sérica día 1 (mg/dl) | 3,7 (2,5) | 3,7 (2,2) | n.s. |
| Creatinina sérica día 30 (mg/dl) | 2,1 (1,7) | 1,8 (1,1) | n.s. |
| Dosis CsA día 1 (mg/kg) | 8,1 (1,4) | 7,1 (1,9) | n.s. |
| Dosis CsA día 30 (mg/kg) | 6,1 (1,6) | 5,8 (1,8) | n.s. |
| Concentración CsA día 1 (ng/ml) | 218,3 (90,6) | 211,2 (75,6) | n.s. |
| Concentración CsA día 30 (ng/ml) | 276,3 (81,8) | 290,8 (73,1) | n.s. |
En ambos grupos el protocolo de inmunosupresión que recibieron los pacientes incluyó la administración de CsA en triple terapia asociada a micofenolato de mofetilo (2 g/día) y prednisona (0,5-1 mg/kg/día) (17, 18). El tratamiento con CsA se inició en las veinticuatro horas siguientes al trasplante, mediante la administración intravenosa de 3-3,5 mg/kg/día, divididos en dos perfusiones intermitentes de seis-ocho horas de duración. Tras veinticuatro-cuarenta y ocho horas, en función de la tolerancia oral del paciente, se introdujo la microemulsión lipídica de CsA por vía oral en dos tomas diarias. La dosis inicial de CsA oral estaba comprendida entre 7 y 10 mg/kg/día y se individualizó de forma progresiva en base al resultado de la concentración sanguínea valle y al ámbito terapéutico predefinido en función del riesgo inmunológico de los pacientes (8). Así se aceptó durante los primeros tres-seis meses concentraciones sanguíneas valle entre 275 y 350 ng/ml y posteriormente entre 200 y 275 ng/ml.
Se incluyeron en el estudio los pacientes que, tras iniciar el tratamiento oral con CsA, se encontraban en situación de estado estacionario; es decir, transcurridas al menos cuarenta y ocho horas desde la última modificación de la posología. Únicamente se consideraron válidas para el estudio las concentraciones sanguíneas extraídas en el momento previo a la siguiente dosis y nunca transcurridas más de catorce horas después de la última administración. Asimismo se excluyeron del estudio a aquellos pacientes que recibían tratamiento concomitante con fármacos inductores e inhibidores enzimáticos por modificar el perfil farmacocinético de CsA.
Toma de muestras y técnica analítica
El seguimiento farmacocinético de los pacientes se realizó mediante monitorización de la concentración sanguínea valle de CsA. Para cada valor de concentración sanguínea de CsA se recogieron simultáneamente los datos correspondientes a la dosis diaria administrada (DD), los días transcurridos desde el trasplante (DPT) y el peso del paciente (P). Las muestras de sangre fueron recogidas sobre tubo de vidrio con EDTA como anticoagulante (Vacutainer®). La determinación de los niveles de CsA se realizó en sangre completa mediante un ensayo de inmunofluorescencia polarizada específico para CsA y sus metabolitos (Abbott, TDx®). La técnica analítica empleada es capaz de determinar concentraciones sanguíneas comprendidas entre 25 y 1.500 ng/ ml. La precisión de la técnica analítica se estudió en este intervalo de concentraciones y el modelo de error resultante, que cuantifica la desviación estándar asociada a cada concentración sanguínea, fue:
Desarrollo del modelo farmacocinético poblacional
El análisis farmacocinético poblacional se ha realizado en el grupo de pacientes de la población A mediante el modelo no lineal de efectos mixtos. La estimación de la tendencia central y de la variabilidad de los parámetros farmacocinéticos se realizó mediante el programa NONMEN (versión IV, nivel 2). Para cuantificar la relación entre la dosis diaria administrada (DD) y la concentración sanguínea de CsA se compararon dos modelos estructurales (tabla 2). Ambos modelos están basados en la ecuación de Michaelis-Menten y sus parámetros farmacocinéticos básicos son la dosis máxima diaria (Dmáx) y la constante de Michaelis-Menten (Km), que representa la concentración sanguínea de CsA en situación de estado embrionario, que se alcanza en el paciente al administrar la mitad Dmáx. La biodisponibilidad y su variabilidad no han sido modeladas, por lo que se consideran implícitas en los parámetros que afectan de modo que éstos alcanzan la característica de aparentes. El modelo 1 es el modelo desarrollado por Grevel et al (5), donde la Km se incrementa de forma lineal a medida que transcurre el tiempo postrasplante hasta alcanzar un valor constante. El modelo 2 se caracteriza por considerar una función creciente no lineal para describir el cambio de Km con respecto al tiempo postrasplante. En ambos modelos el valor de Km se encuentra normalizado por el peso corporal del paciente.
| Tabla 2. Modelos utilizados para describir el comportamiento farmacocinético de CsA y el valor de sus parámetrosde tendencia central y variabilidad | |||
| Modelo estructural | Ecuación | Parámetro | Media (ES) |
| Modelo 1 | 
| Dmáx (mg/kg/día) Km (ng/ml/kg) T (días) 
| 9,38 (0,71) 4,0 (0,6) 46 (5) 7 (14) 53 (32) 0,51 (0,24) |
| Modelo 2 | 
| Dmáx (mg/kg/día) Km (ng/ml/día) B (días1) (%) 
| 9,92 (0,51) 5,57 (0,77) 0,0236 (0,0035) 18 (11) 50 (32) 66 (42) 0,49 (0,15) |
DD: dosis total diaria (mg/kg). C: concentración sanguínea valle de CsA (ng/ml). Dmáx: dosis máxima diaria. Km: constante de Michaelis-Menten. DPT: días postrasplante. T: tiempo a partir del cual la Km es independiente de DPT. La variable A toma el valor de DPT cuando DPT es menor que T y si DPT es mayor que T, A toma el valor de T. 
| |||
Se asume que la dosis diaria estimada se encuentra sujeta a un error residual aditivo que se puede expresar de la siguiente forma (ecuación 1):
donde DDij es la dosis diaria administrada al paciente j-ésimo el día j-ésimo, DDij* es la dosis diaria estimada por el modelo en el paciente i-ésimo el día j-ésimo, y
donde Pi es el parámetro farmacocinético del individuo i-ésimo, P es el parámetro farmacocinético poblacional de tendencia central, y
Como criterio para la selección del modelo se utilizó el valor de la función mínima objetivo (FMO), la modificación en la precisión de la estimación de los parámetros a través del error estándar, la disminución de la variabilidad interindividual e intraindividual y la ausencia de correlaciones entre los parámetros estimados. Además se comprobaron las asunciones realizadas mediante el análisis de las representaciones gráficas de los residuales ponderados frente a las predicciones realizadas y los gráficos de dispersión de las dosis diarias observadas frente a las predicciones realizadas a priori y a posteriori en cada modelo.
Estimación de parámetros farmacocinéticos individuales
En el grupo de pacientes de la población B se realizaron las predicciones de dosis diarias de CsA a través de la estimación de parámetros farmacocinéticos individuales. La estimación de los parámetros farmacocinéticos individuales se realizó mediante la metodología bayesiana que permite describir la relación cuantitativa existente entre la probabilidad a priori de que el paciente presente ciertos valores de parámetros farmacocinéticos cuando no se conocen sus concentraciones sanguíneas, y la subsiguiente probabilidad a posteriori de tener semejantes valores de parámetros después de conocer las concentraciones sanguíneas:
donde prob(P/C) es la distribución de probabilidad a posteriori de los parámetros farmacocineticos P en función de las concentraciones sanguíneas medidas C; prob(P) es la probabilidad de que los parámetros del paciente asuman la distribución de los parámetros poblacionales; prob(C/P) es la distribución de probabilidad de las concentraciones medidas en el contexto del modelo farmacocinético y de los errores de medida, y prob(C) es la distribución de probabilidad de las concentraciones medidas.
Los parámetros farmacocinéticos poblacionales obtenidos con el modelo 2 en la población A se utilizaron como información poblacional a priori. Cuando la función de distribución de probabilidad de los parámetros farmacocinéticos no es significativamente distinta de una distribución log-normal, como sucede en este caso, la máxima probabilidad a posteriori de que un paciente presente una determinada concentración sanguínea cuando se administra una determina dosis diaria, se alcanza con los parámetros farmacocinéticos que minimizan la ecuación 4:
donde DDij es la dosis diaria administrada al paciente i-ésimo el día j-ésimo, DDij* es la dosis diaria estimada por el modelo en el paciente i-ésimo el día j-ésimo, P representa los m parámetros farmacocinéticos poblacionales de tendencia central, Pi son los m parámetros farmacocinéticos individuales estimados y * es el coeficiente de variación del parámetro farmacocinético n. IW es el factor de ponderación de las observaciones; en este caso, puesto que el modelo de varianza residual, del modelo farmacocinético poblacional es aditivo (ecuación 1) IW toma el valor de cero. FF es el factor de ponderación de los datos del paciente respecto a los datos poblacionales, que toma valores comprendidos entre 0 y 1; su valor óptimo puede calcularse a partir de la ecuación 5 propuesta por Yamaoka et al (19):
donde
La estimación de los parámetros farmacocinéticos individuales se realizó, cada vez que se disponía de un nuevo valor de concentración sanguínea de CsA, a través de la minimización de la FMOBay (ecuación 4), mediante mínimos cuadrados según el algoritmo de Gauss-Newton implementado en el programa MULTI2 (BAYES) (19). De esta forma es posible validar el procedimiento de individualización posológica a partir de la determinación de CsA en el paciente.
Evaluación de la capacidad predictiva
La exactitud y la precisión en la estimación de la dosis diaria a administrar se evaluó mediante la teoría de errores de predicción de Sheiner y Beal (20). Como parámetro de exactitud se calculó la media del error de predicción relativo (ERM) existente entre las dosis diarias administradas y las dosis diarias estimadas mediante la metodología bayesiana (ecuación 6). Como parámetro de precisión se calculó la desviación estándar del error de predicción (DEER) mediante la ecuación 7:
La estimación bayesiana de la dosis diaria a administrar no es una estimación exacta, sino que va acompañada de un error derivado del proceso de estimación de los parémetros farmacocinéticos individuales. Este error no es contemplado en el cálculo de los parámetros que valoran la exactitud y la precisión de la teoría de Sheiner y Beal. En este sentido, Vozeh et al sugieren evaluar la capacidad predictiva de un modelo farmacocinético mediante el error de predicción estandarizado (21). Si la función de distribución de probabilidad del error de predicción estandarizado es normal, la media de esta distribución no será significativamente distinta de cero y su desviación estándar no será significativamente distinta de 1. Estas dos propiedades permiten la evaluación de la exactitud y la precisión de un método predictivo y su comparación con otros métodos. La media (ESM) y la desviación estándar (DEES) del error de predicción estandarizado se calculó mediante las siguientes ecuaciones 8 y 9:
RESULTADOS Y DISCUSION
La menor variabilidad farmacocinética de la nueva presentación oral de CsA (Sandimmun Neoral®) ha propiciado una relación lineal entre dosis administradas y AUC (13, 14) que permite utilizar las concentraciones sanguíneas valle de CsA como un indicador preciso de la exposición sistémica al fármaco (22, 23).
La caracterización del comportamiento farmacocinético de CsA, mediante el modelo de efectos mixtos, no ha sido tratada extensamente en la bibliografía especializada. Tan sólo Grevel en 1993 desarrolló un modelo farmacocinético poblacional en pacientes portadores de un injerto renal y subsidiarios de tratamiento individualizado con CsA mediante la monitorización del área bajo la curva (5). En nuestra población se evaluó el modelo de Grevel (modelo 1) y se comparó con un modelo alternativo desarrollado por nosotros (modelo 2). El modelo 2 describe mejor que el modelo 1 la relación entre la dosis diaria administrada y la concentración de CsA. En efecto, en la tabla 2 donde se muestran los valores de los parámetros farmacocinéticos poblacionales, estimados con ambos modelos y sus respectivos valores de error estándar, se puede observar lo antedicho.
La precisión en la estimación de los parámetros de tendencia central es inferior al 25% y la correspondiente a los parámetros de variabilidad inter e intraindividual se sitúan alrededor del 50%. Además, las correlaciones entre parámetros son inferiores a 0,75. En conjunto, estos resultados son compatibles con una buena exactitud y precisión en la estimación de los parámetros farmacocinéticos poblacionales, tanto de tendencia central como de variabilidad.
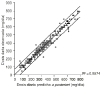
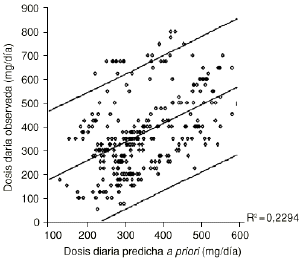
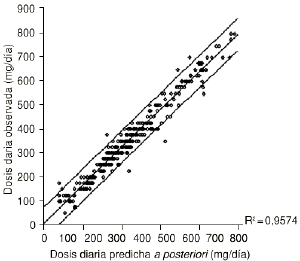
Para evaluar el beneficio potencial del desarrollo de un método bayesiano de estimación de parámetros farmacocinéticos individuales, en la población A se han comparado las dosis diarias predichas a priori por el modelo 2, utilizando el valor medio de los parámetros farmacocinéticos poblacionales, con las predicciones a posteriori, realizadas mediante la metodología bayesiana implementada en NONMEN (Fig. 1). En este último caso se ha utilizado toda la información disponible del paciente para la estimación de los parámetros farmacocinéticos individuales. De esta forma la variabilidad residual existente entre las dosis predichas por el modelo 2 y las dosis administradas a los pacientes se reduce alrededor del 70% al caracterizar los parámetros farmacocinéticos de cada paciente de forma individual. Este valor justifica por sí mismo el desarrollo de un método bayesiano de estimación de parámetros farmacocinéticos individuales.
Figura 1.--Diagrama de dispersión de la dosis diaria observada frente a dosis diaria predicha a priori (A) y dosis diaria predicha a posteriori (B) en la población A.
La estimación de parámetros farmacocinéticos individuales mediante la metodología bayesiana combina la información de los parámetros poblacionales y la información propia del paciente. De esta forma se evita que las predicciones realizadas difieran significativamente de la media poblacional y se minimiza el efecto de concentraciones sanguíneas erróneas. Por otro lado, una ventaja adicional que este método presenta es su utilización aun cuando sólo se disponga de un único valor de concentración plasmática (11).
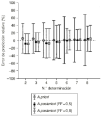
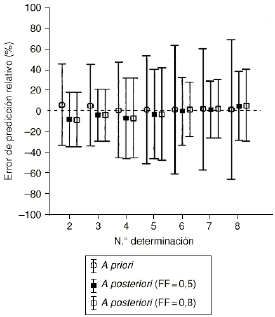
En la población B, las dosis de CsA predichas por el modelo 2 se han calculado a priori utilizando el valor medio de los parámetros farmacocinéticos poblacionales, y a posteriori, mediante la tecnología bayesiana, considerando los valores de FF de 0,5 y 0,7. En este último caso para la estimación de los parámetros farmacocinéticos individuales se ha considerado la información disponible del paciente tras cada monitorización de su concentración sanguínea. En la figura 2 se muestra el ERM y su intervalo de confianza del 95% (ERM ± 1,96 DEER) para la predicción a priori y a posteriori para los dos valores de FF analizados en este estudio. La figura evidencia la excelente exactitud tanto de la predicción a priori como de la predicción a posteriori ya que en cualquier monitorización el ERM no es significativamente distinto de 0. En cuanto a la precisión, se pone de manifiesto la progresiva disminución del intervalo de confianza del 95% de ERM de las predicciones a posteriori a medida que se dispone de mayor número de concentraciones sanguíneas de CsA de los pacientes. Todo lo contrario sucede en el caso de las predicciones a priori, donde el intervalo de confianza del 95% de ERM se incrementa a medida que aumenta el número de concentraciones sanguíneas de CsA como era de esperar.
Figura 2.--ERM (%) e intervalo de confianza del 95% de la predicción a priori y a posteriori realizada en la población B para los valores de FF de 0,5 y 0,8 en función del número de orden de determinación sanguínea de CsA.
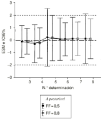
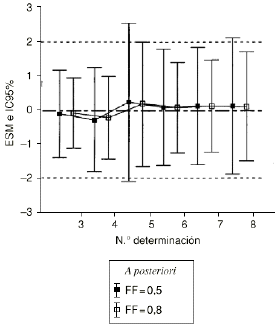
La exactitud y la precisión de la estimación a posteriori, cuantificada mediante ERM y DEER, no difiere significativamente entre los valores de FF de 0,5 y 0,8. Ahora bien, la utilización de ESM y la DEES, como parámetros de exactitud y precisión, respectivamente, permite establecer que la exactitud de ambos métodos predictivos es similar puesto que ESM no difiere significativamente de 0 en ningún caso (Fig. 3). No obstante, se evidencia como el intervalo de confianza del 95% del ESM es inferior a 1,96 en más del 80% de los casos. Según Vozeh et al estos hallazgos sugieren que el error estándar de la predicción de la dosis diaria a administrar es excesivo para garantizar una buena precisión de la estimación, particularmente cuando el valor de FF es de 0,8. Estos hechos, imputables a la no linealidad del modelo y a la elevada variabilidad interindividual de los parámetros farmacocinéticos de CsA, bien por la influencia del tiempo postrasplante u otros factores, justifican la realización de nuevos estudios que evalúen la utilidad de disponer de un modelo bayesiano en la individualización posológica de pacientes con trasplante renal.
Figura 3.--ESM e intervalo de confianza del 95% de la predicción a posteriori realizada con el método bayesiano en la población B para los valores de FF de 0,5 y 0,8 en función del número de orden de determinación sanguínea de CsA.
BIBLIOGRAFIA
1.Kahan BD. Pharmacokinetic considerations in the therapeutic application of cyclosporine in renal transplantation. Transplant Proc 1996;28:2141-3.
2.Parke J, Charles BG. NONMEN population pharmacokinetic modeling of orally administered cyclosporine from routine drug monitoring data after heart transplantation. Ther Drug Monitor 1998;20:284-93.
3.Tsumoda SM, Aweeka FT. The use of therapeutic drug monitoring to optimise immunosuppresive therapy. Clin Pharmacokinet 1996;30:107-40.
4.Lindholm A, Dahqvist R, Groth CG, Sjöqvist F. A prospective study of cyclosporine concentration in relation to its therapeutic effect and toxicity after renal transplantation. Br J Clin Pharmacol 1990;30: 443-52.
5.Grevel J, Post BK, Kahan BD. Michaelis-Menten kinetics determine ciclosporine steady-state concentrations: a population analysis in kidney transplant patients. Clin Pharmacol Ther 1993;651-60.
6.Sallas WM. Development of limited sampling strategies for characteristics of a pharmacokinetic profile. J Pharmacokinetic Biopharm 1995;23:515-29.
7.Gasoari F, Anedda MF, Signori O, Remuzzi, Perico N. Prediction of cyclosporine area under the curve using three-point sampling strategy after Neoral administration. J Am Soc Nephrol 1997;8:647-52.
8.Oellerich M, Armstrong VW, Kahan B, et al. Lake Louise consensus conference on cyclosporin monitoring in organ transplantation: report of the consensus panel. Ther Drug Monit 1995;17:642-54.
9.Costa X, Cantarrell C, Capdevilla L, López R, Pascual C, Pou L. Estimación del área bajo la curva de concentración-tiempo de ciclosporina A mediante una estrategia de muestreo limitado. Aten Farm 1999;1:16-22.
10.Charpiat B, Falconi I, Bréant V, Jelliffe RW, Sab JM, Ducerf C, et al. A population pharmacokinetic model of cyclosporine in the early postoperative phase in patients with liver transplants, and its predictive performance with bayesian fitting. Ther Drug Monitor 1998;20:158-64.
11.Peck CC, Rodman JH. Analysis of clinical pharmacokinetic data for individualizing drug dosage regimens. En: Evans WE, Schentag JJ, Jusko WJ. Applied pharmacokinetics. Spokane: Ed. Applied Therapeutics; 1992.
12.Anderson JE, Munday AS, Kelman AW, Whiting B, Briggs JD, Knepil J, Thomson AH. Evaluation of a bayesian approach to the pharmacokinetic interpretation of cyclosporin concentrations in renal allograft recipients. Ther Drug Monit 1994;16:160-5.
13.Friman S, Backman L. A new microemulsion formulation of ciclosporin. Pharmacokinetic and clinical features. Clin Pharmacokinet 1996;30:181-93.
14.Jiménez NV, Casabó VG, Sancho V. Manual de procedimientos para farmacocinética clínica, 1.a ed. Valencia: AFAHPE; 1997. p. 29-40.
15.Porta B, Pérez-Ruixo JJ, Jiménez NV, Sancho A, Pallardo LM. Individualización posológica de ciclosporina en pacientes con trasplante renal: propuesta de un modelo farmacocinético de predicción. Farm Hosp 1998;22:181-7.
16.Bellisant E, Sébille V, Paintaud G. Methodological issues in pharmacokinetic-pharmacodinamic modelling. Clin Pharmacokinetic 1998;35:151-66.
17. Sollinger HW. Mycophenolate mofetil for the prevention of acute rejection in primary cadaveric renal allograft recipients. Transplantation 1995;60: 225-32.
18.The tricontinental mycophenolate mofetil renal transplantation study group. A blinded, randomized clinical trial of mycophenolate mofetil for the prevention of acute rejection in cadaveric renal transplantation. Transplantation 1996;61:1029-37.
19.Yamaoka K, Nakagawa T, Tanaka H, Yasuhara M, Okumura K, Hori R. A nonlinear multiple regression program, multi2 (Bayes), based on algoritm for microcomputers. J Pharmacobio-Dyn 1985;8:246-56.
20.Sheiner LB, Beal SL. Some suggestions for measuring predictive performance. J Pharmacokinetic Biopharm 1981;9:502-12.
21.Vozeh S, Uematsu T, Hauf GF, Follath F. Performance of bayesian feedback to forecast lidocaine serum concentration: evaluation of prediction error and the prediction interval. J Pharmacokinetic Biopharm 1985;13:203-12.
22.Kovarik JM, Mueller EA, Van Bree JB, Tetzhoff W. Reduced inter and intraindividual variability in cyclosporin pharmacokinetics from microemulsion formulation. J Pharma SCI 1994;83:444-6.
23. Mueller EA, Kovarik JM, Van Bree JB, Tetzhoff W, Grevel, Kutz K. Improved dose linearity of cyclosporin pharmacokinetics from a microemulsion formulation. Pharm Res 1994;11:301-4.
